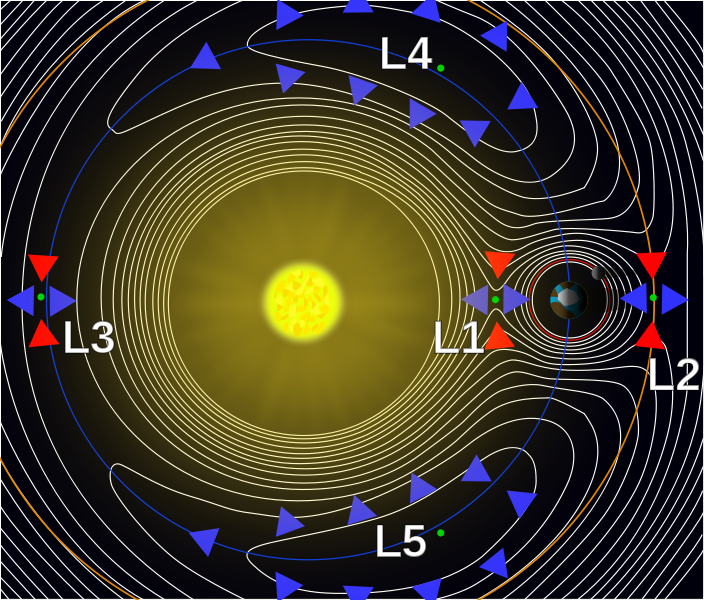
The case in which one of the bodies has negligible mass is called the restricted three-body problem. Dynamics is complicated even in this case, however, there are exact solutions at least for equilibrium points. These so-called Lagrangian points (see figure to the left; source: Physics Stack Exchange) corotate with with binary made up of the other two point masses.
In my first scientific project I investigated how the well-known Lagrangian points are modified if the potential between the two massive bodies is altered from the classical Newtonian 1/r to onw with ~r^2 (a harmonic oscillator potential). This could be a very simple model for two prestellar clumps moving in a molecular cloud. Assuming physical parameters there turns out to be a stable equilibrium point, which might help star formation as cold clupms can get together there. See our paper here.
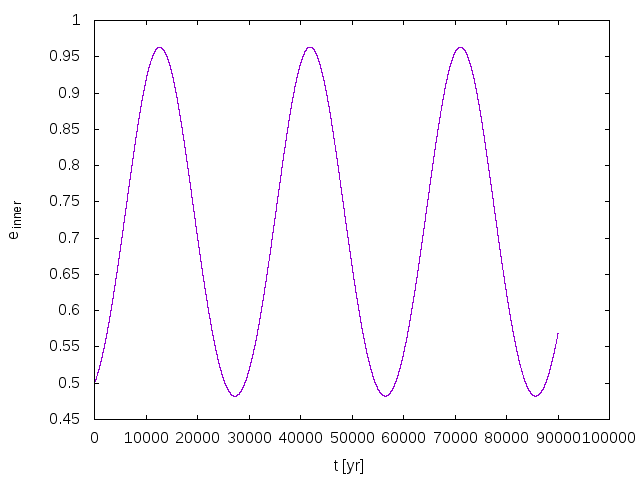
The case in which our triple is divided into a tight inner binary (two bodies) and a wide outer binary (a third body + the barycenter of the inner binary) is called the hierarchical three-body problem. The tertiary perturbs the inner binary, which orbital elements therefore vary in time. For instance, the eccentricity exhibits oscillations on very long (secular) timescales (see the figure to the left). This phenomenon was first studied by von Zeipel in 1910 and by Lidov and Kozai in 1961-62 so it has been named in their honor.
In our research group, called Galnuc, we investigate the dynamics of dense stellar clusters in galactic nuclei. We have shown that a small population of intermediate-mass black holes could significantly decrease the number of compact object binaries in the nucleus by perturbing them until their orbits become Hill unstable with the central supermassive black hole. For more details see our paper here.

The Zepiel-Lidov-Kozai (ZLK) mechanism induces large-amplitude oscillations in the orbital elements of a perturbed binary. The variations of eccentricity can modulate the gravitational wave signal detected by the future space telescope LISA.
If one of the members of the binary is an intermediate-mass black hole, then the general relativistic effects can dominate over the ZLK mechanism, i.e. the apsidal precession may completely wash away the eccentricity peaks. However, in some parts of the parameter space (illustrated by the figure on the left), the modulation of the wave signal can be still detected. For more details see our paper here.
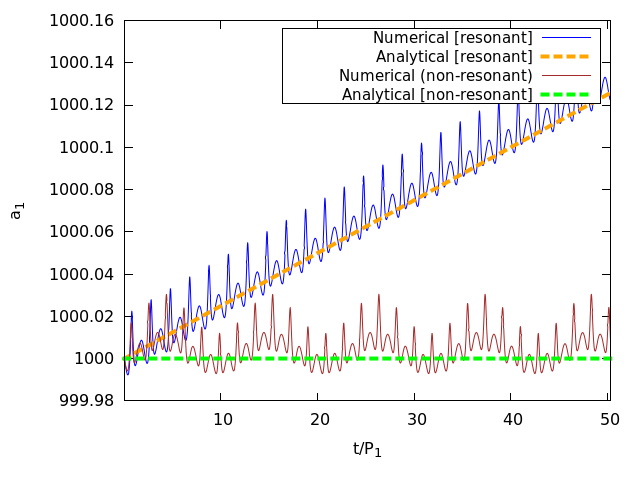
The essence of the ZLK mechanism is that it ignores those effects that occur within the orbital period of the binary and instead it describes the long-term, secular evolution. Technically, one averages the perturbing Hamiltonian of the system, which is a canonical transformation. This transformation is generated by a function which diverges if the orbital frequencies of the inner and outer binares are commensurate.
In this paper we propose another generating functions which is not subject to this technical difficulty. With this function one is able to execute the orbit averaging even in mean motion resonaces, however, the transformed orbital elements lose their original geomtrical meaning. For more details see our paper here.
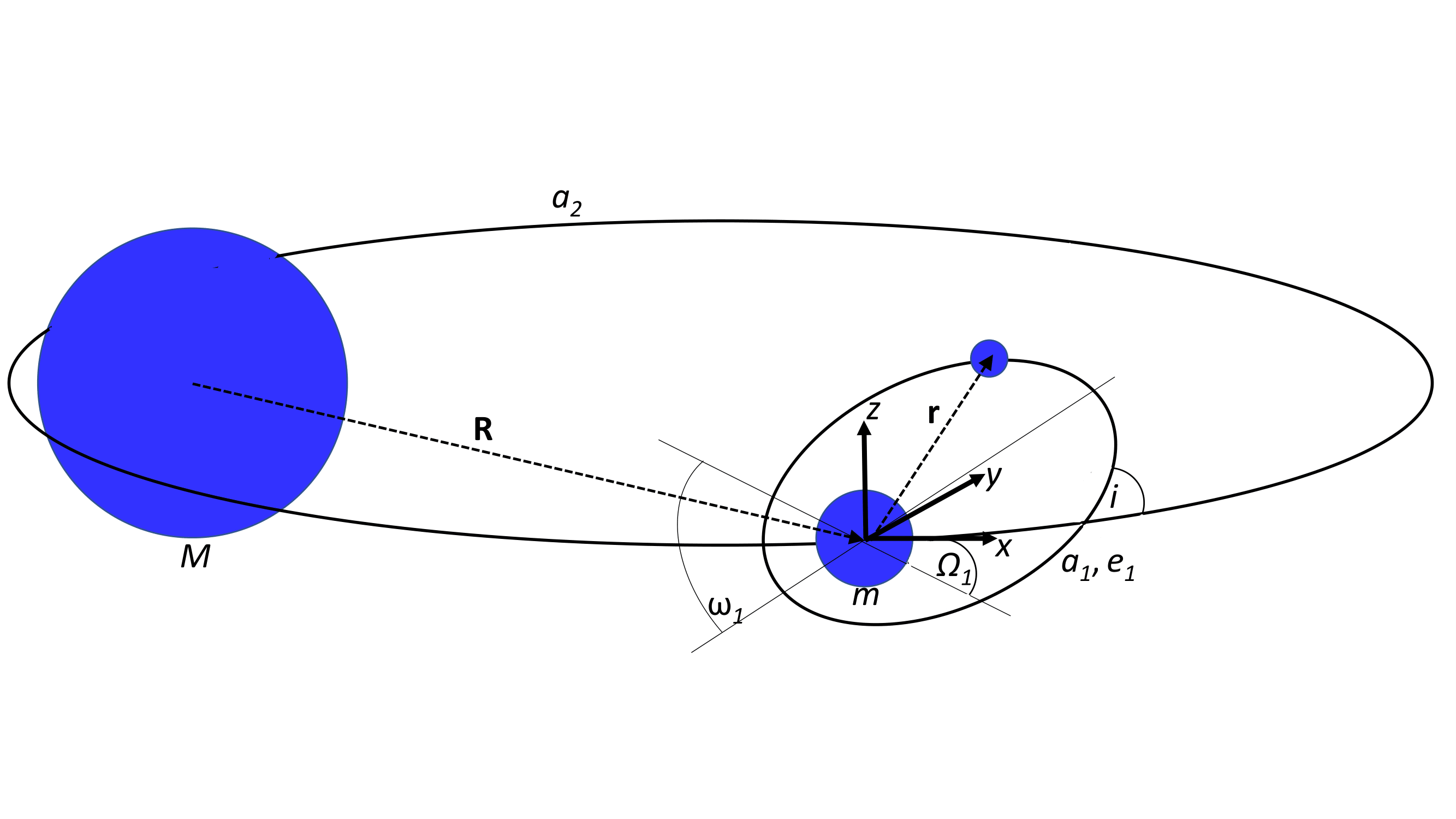
The standard way to derive the dynamical nature of the ZLK mechanism is within the framework of Hamiltonian mechanics. One constructs the perturbing hamiltonian function from first principles, averages over the orbital periods and then insert the obtained perturbation into the Lagrangian planetary equations. This procedure is elegant and very powerful, however, may not be an easy-to-follow path for those who first encounter this phenomenon (at least this is what I experienced a couple of years ago).
In this paper I derive the same results but build on the more familiar concepts of force and torque vectors, i.e. "F=ma" and "T=r×F". For more details see my paper.